
After applying the rotation the Cartesian coordinates will be x’ and y’, θ is the angle of rotation. The following two equations results x and y are the Cartesian coordinates of a point before applying the rotation. Here is the clearer version: The 'formula' for a rotation depends on the direction of the rotation. I hope this helps Edit: I'm sorry about the confusion with my original message above. The multiplication of matrix technique is use to solve the problems If you want to do a clockwise rotation follow these formulas: 90 (b, -a) 180 (-a, -b) 270 (-b, a) 360 (a, b). The rotation matrix is use to calculate the coordinates of a point when applying a 2D rotation of a set angle θ 1) rotation 180 about the origin x y N F P K 2) rotation 180 about the origin x y J V R Y 3) rotation 90 counterclockwise about the origin x y N B X 4) rotation 90 clockwise about the origin x y U Y K B 5) rotation 90 clockwise about the. In revolution, orbital motion takes place around another object. Rotations Date Period Graph the image of the figure using the transformation given. Step 2: Apply the 180-degree rule to each given point to get the new. In rotation, an object spinning motion in its own axis. Note: Rotating a figure 180 degrees counterclockwise will have the same result as rotating the figure 180 degrees clockwise. The following example is about square, and its rotation is counterclockwise (or clockwise) 90?, 180? and 270? respectively.ĭifference between Rotation and revolution Rotated270 = cv2.warpAffine(img, M, (h, w))Ĭv2.waitKey(0) # waits until a key is pressedĬv2.destroyAllWindows() # destroys the window showing imageĬv2.imshow('Image rotated by 90 degrees',rotated90)Ĭv2.imshow('Image rotated by 180 degrees',rotated180)Ĭv2.imshow('Image rotated by 270 degrees',rotated270)Ĭv2.Rotation symmetry exists only when rotation of shape is less than 360? M = cv2.getRotationMatrix2D(center, angle270, scale) To improve this New coordinates by rotation of points Calculator, please fill in questionnaire. Quadrants We know that a cartesian plane has four quadrants and each quadrant has a specific sign convention for the x and y coordinates. Rotated180 = cv2.warpAffine(img, M, (w, h)) Most commonly used rotations are 90 o, 180 0 and 270 o in a clockwise or counter-clockwise direction with respect to the origin ( 0, 0). M = cv2.getRotationMatrix2D(center, angle180, scale) One of the simplest and most common transformations in geometry is the 180-degree rotation, both clockwise and counterclockwise. Rotated90 = cv2.warpAffine(img, M, (h, w)) Find an image of the point (3, 2) that has undergone a clockwise rotation. M = cv2.getRotationMatrix2D(center, angle90, scale) # Perform the counter clockwise rotation holding at the center

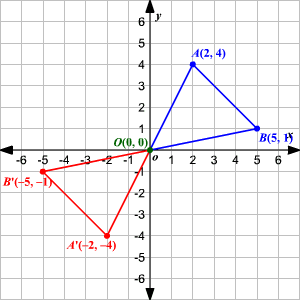
Img = cv2.imread('/home/arjun/Desktop/logos/python.png') For each rotation with given degrees, we will save the image. rotating triangle CDE 180 degrees clockwise, the (x,y) coordinates are opposite. Example 1 : Let P (-2, -2), Q (1, -2), R (2, -4) and S (-3, -4) be the vertices of a four sided closed figure. In this example, we will read an image, and then rotate it different angles liek 90 degrees, 180 degrees and 270 degrees. Quadrant 3 to 2 when rotating 180 degrees clockwise. When we rotate a figure of 180 degrees about the origin either in the clockwise or counterclockwise direction, each point of the given figure has to be changed from (x, y) to (-x, -y) and graph the rotated figure. swap height with width and width with height. When you are rotating by 90 or 270 and would to affect the height and width as well. Ask students why it is not necessary to specify the direction of a 180 degree rotation (because a 180 degree clockwise rotation around point has the same effect.

Note: Please observe that the dimensions of the resulting image are provided same as that of the original image.
Although the rotation of images seems to be a complicated operation to be implemented through coding, it is still one of the most commonly needed patients, especially when dealing with problems specific to image processing and transmission. Other value scales the image by the value provided. The image rotated at 180 degree, which a mirror image of the original image. scale: 1.0 mean, the shape is preserved.rotated: ndarray that holds the rotated image data.angle: angle by which image has to be rotated in the anti-clockwise direction.center: center of the image (the point about which rotation has to happen).Syntax – cv2: rotate image M = cv2.getRotationMatrix2D(center, angle, scale)


 0 kommentar(er)
0 kommentar(er)
